序

这是北京航空航天大学计算机学院 2025 年计算机组成原理预习部分的 Logisim 部分。

什么是 Logisim？

Logisim 是一款非常优秀的用于数字电路设计与仿真的教育软件。它提供了丰富的电路库与元件的抽象表示，生成的电路图也比较美观，还提供了时序的模拟功能，能够让我们对 CPU 的结构和运行情况有更直观的理解，并且在开发一些小电路时还有一些其他辅助功能。
为什么要学习 Logisim？

这里有什么？

Logisim 门电路
Logisim 组合电路
Logisim 时序电路
Logisim 仿真与调试
应用与挑战

Logisim 门电路

界面认识

打开 Logisim 后，我们会看到如下的界面：

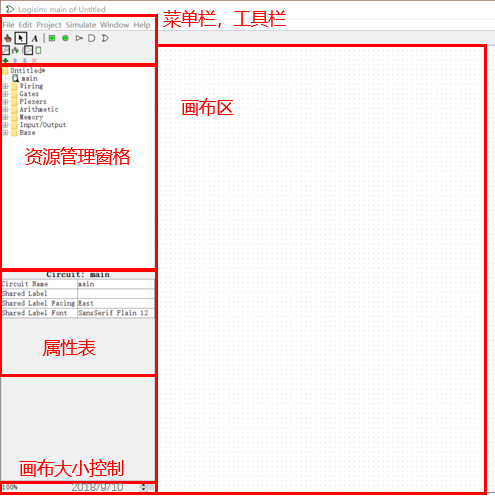
Logisim 提供图形界面，可以通过长按拖动的形式新建部件以及进行连线。也可通过 Ctrl + D 快速部署选中的部件。

元件概览

Wirings（线路）

Tunnel（隧道）

Tunnel 部件是在整个 Logisim 实验中简化电路布线复杂度效果最好的一个部件，可以让你在纷繁复杂的接线中解脱出来，让你能够更加专心的关注于各个部件的设计，而不被复杂的接线所打扰。
Tunnel 名为隧道，即它可以将标签相同 Tunnel 之间的数据，通过一个不可见的“隧道”进行传输，在使用过程中，可以链接数据的输入端和输出端，使得数据可以方便简单的传输。^[1]

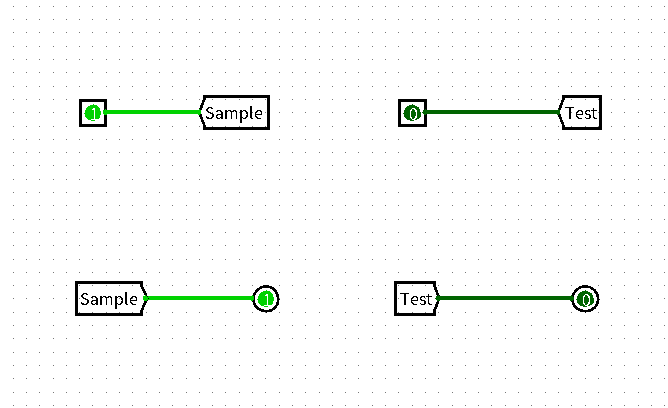
拥有不同标签的 Tunnel 之间，数据传输是独立的。

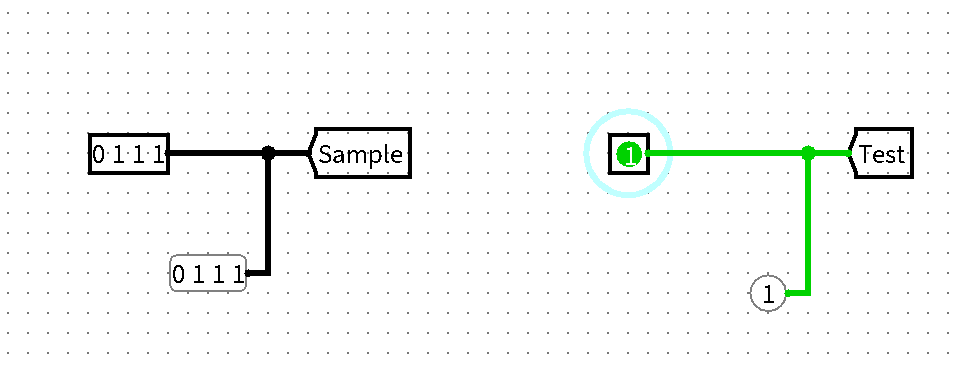
Probe（探针）

Probe 作为一个显示线路数据值的部件，可以对多位宽数据进行实时监控，简而言之，就是可以直接显示接线的数值，并且不影响整个电路的运行。
Probe 有点类似于输出引脚，可以显示数值，它可以显示多位宽数据。

Splitter（分叉器）

Splitter 是一个多路分叉器，可以将一个数据输入端分成多个输出端，可以将数据进行分流，使得数据可以分别处理。每条岔路都会注明数据来源的位编号，位编号从 0 开始，对应数据源最靠右的位，例如：

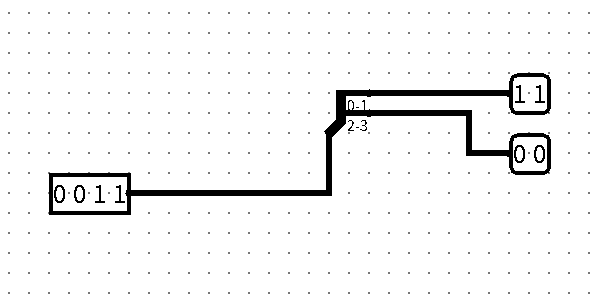
要注意，Splitter 分流后，数据的位宽会相应的发生改变，因此输出引脚的位宽也需要改变。

Splitter 的输出引脚也可以当输入来用，这时，原先的输入引脚会输出此时输入的数据的组合（按照位次顺序）。

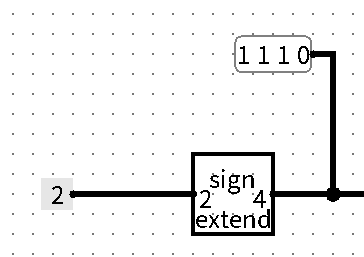
Bit Extender（位扩展）

Bit Extender 有三个主要的参数：

Bit Width In：输入数据的位宽
Bit Width Out：输出数据的位宽
Extension Type：扩展方式，包括 Zero, One, Sign, Input。

当输入数据的位宽小于输出数据的位宽时，Bit Extender 保留全部输入数据，然后补充内容使得输出数据位宽达到要求。

若 Extension Type 为 Zero，则补充 0。
若 Extension Type 为 One，则补充 1。
若 Extension Type 为 Sign，则补充符号位^[2]。

当输入数据的位宽大于输出数据的位宽时，Bit Extender 从低到高截取需要的位数，其余的舍弃。

Clock（时钟）

在 Simulate 菜单中开启 Ticks Enabled 选项，Clock 会自动经历周期，释放信号。
Clock 可以指定 High Duration 和 Low Duration，分别表示高电平持续时间和低电平持续时间。单位为 Tick(s)。

Logisim 对时钟的模拟是理想状态的：在实际电路中，多个时钟会相互漂移，并且永远不会同步移动。但在 Logisim 中，所有时钟都以相同的速率经历滴答声。

Clock 的周期：

Gates（门）

Odd Parity（奇校验）

奇校验门和异或门在两个输入端时表现相同。但是如果有超过两个指定的输入，异或门将在刚好++只有一个 1 的时候输出 1。而奇校验门在奇数个 1 ++输入时就会输出 1。

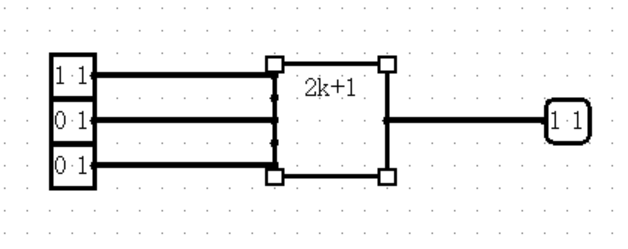
第一列和第二列均为奇数个 1，则输出端的第一列和第二列均为 1。

这与异或门的 Multiple-Input Behavior 字段选择 When an odd number are on 是一致的，而其默认选项是 When one input is on （只有一个 1 时输出 1）。

Even Parity（偶校验）

偶校验门在输入端有偶数个 1 时输出 1，否则输出 0。

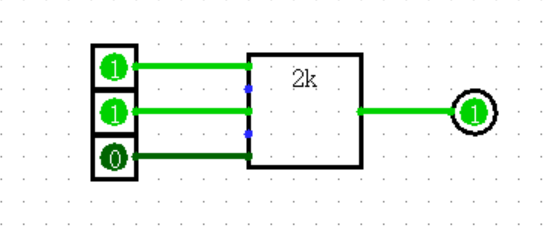
Plexers（复用器）

Multiplexer(MUX)（多路选择器）

在组合电路中，多路选择器（Multiplexer，简称 MUX）是非常重要的一类部件，他们在组合电路中扮演着非常重要的角色。下图是一个典型的 Logisim 中的多路选择器，左侧是多个输入，右侧是相应的输出，通过底部（黑色）的选择信号，对输入的信号进行选择后输出。另外一个端口是部件的使能端，当其为高电平（为 1）时，整个部件使能工作。

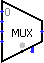
选择信号：当 Select Bits 字段为 n 时，选择信号的位宽为 n，此时输入引脚有 2ⁿ 个。选择信号的值表示选择要输出的输入信号的位次，自上而下，从 0 开始。

Demultiplexer(DMX)（多路分配器）

多路分配器和多路选择器功能恰好相反，即能够将 1 个输入数据，根据需要传送到多个输出端的任何一个输出端。

选择信号：当 Select Bits 字段为 n 时，选择信号的位宽为 n，此时输出引脚有 2ⁿ 个。选择信号的值表示选择要把输入信号复制到第几个输出引脚上，自上而下，从 0 开始。

Decoder（译码器）

如下图，右侧是多个输出，底部是黑色的选择信号与使能端。译码器最大的功能在于将二进制编码转换为相应的独热码（one-hot），如 101 的 3 位二进制编码作为输入就会被转换成 00100000 的 8 位独热码作为输出。因而该元件得名译码器。

译码器与多路选择器不同之处有两点：

除选择信号外，多路选择器是多输入，单输出，输出取决于输入与选择信号，译码器则是无输入，多输出，输出模式仅取决于选择信号。
译码器输出位宽每个信号仅一位，多路选择器可以有多位。

Bit Selector（位选择器）

Bit Selector 有两个重要的参数：

Data Bits: 输入数据的位宽
Output Bits: 输出数据的位宽
Bit Selector 有两个输入：data 和 dist。其中，dist 宽度为 ⌈log₂(⌈data / Output Bits⌉)⌉。
一个输出为 Output Bits 位宽。
Bit Selector 根据输出数据的位宽将输入数据等分成若干段，每段为 Output Bits 位宽。然后根据 dist 指定的编号从低到高选出需要的段并输出。

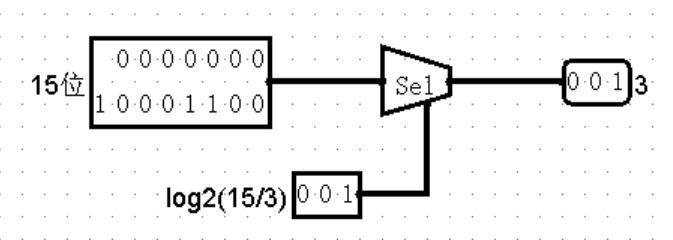
Arithmetic（运算器）

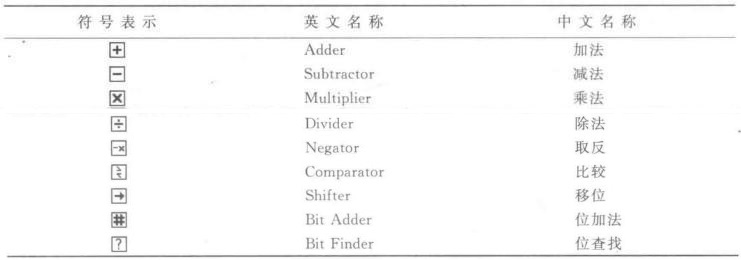
Negator（取反）

Negator 是一个单输入的运算器。名曰取反，实则求补。即取反加一。

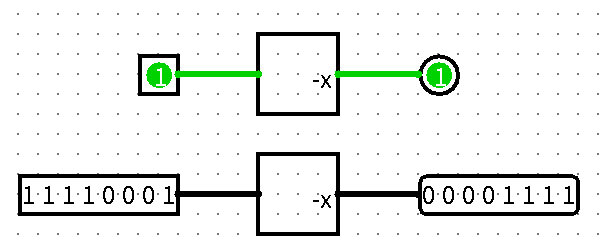
Shifter（移位）

Shifter 含有两个输入，data 和 dist，它有一个输出，这是根据 dist 位移动数据的结果。data 和输出具有相同的位宽。

data 的位宽和 dist 的位宽需要满足下述数学关系：
dist = ⌈log₂data⌉

Shifter 支持以下几种移位方式：

Logical Left（逻辑左移）: 数据中的所有位向左移动 dist 位，底部空出的位用 0 填充。例如，11001011逻辑左移两次就是00101100（之前的右边两位丢弃）。
Logical Right（逻辑右移）: 数据中的所有位向右移动 dist 位，左端空出的位用 0 填充。例如，11001011逻辑右移两次就是00110010（之前的左边两位丢弃）。
Arithmetic Right（算术右移）: 数据中的所有位向右移动 dist 位，左端空出的位用数据中最高位重复填充。例如，11001011算术右移两次就是11110010（之前最高位为 1，所以用 1 填充）。
Rotate Left（循环左移）: 数据中的所有位都向左移动 dist 位，左边被“挤出去”的位填充到右边空出的位。例如，将11001011循环左移两次就是00101111。
Rotate Right（循环右移）: 数据中的所有位都向右移动 dist 位，右边被“挤出去”的位填充到左边空出的位。例如，将11001011循环右移两次就是11110010。

本小节摘自 CSDN

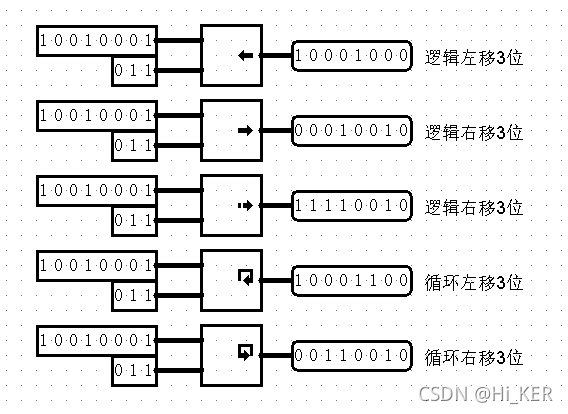
Bit Finder（位查找）

Bit Finder 有一个 n 位宽的输入，有一个 1 位宽的输出，表示在输入中是否找到对应的值。对于 n 位的输入，Bit Finder 有一个 ⌈log₂n⌉ 位宽的输出表示找到的值的编号。
Bit Finder 有一个 Type 参数：

Lowest-order 1: 自最低位开始查找 1
Highest-order 1: 自最高位开始查找 1
Lowest-order 0: 自最低位开始查找 0
Highest-order 0: 自最高位开始查找 0

无论何种查找方式，返回的都是绝对位次，即从右往左数从 0 开始的位次。

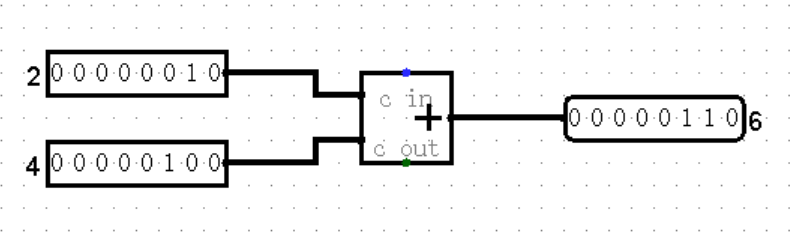
Adder（加法）

Adder 将两个左端输入值数学相加，并在右端输出结果。

Subtractor（减法）

Subtractor 将两个左端输入值数学相减，并在右端输出结果。

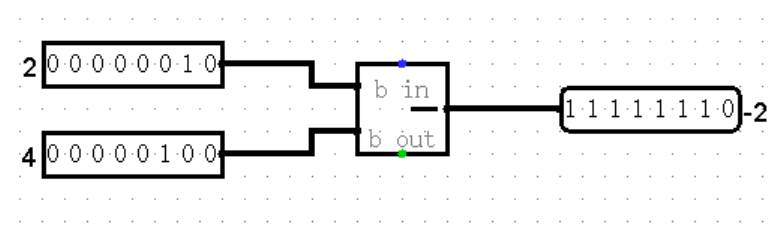
差值为负，则结果为其补码。

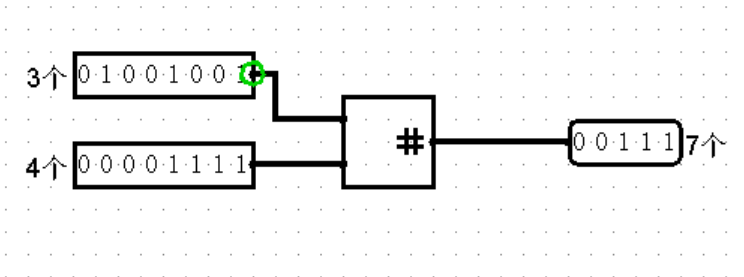
Bit Adder（位加法）

Bit Adder 计算输入中有多少位是 1，并输出为 1 的位的数量。对于 n 位的输入，Bit Adder 有一个 ⌈log₂n⌉ 位宽的输出表示 1 的位的数量。

Bit Adder 可以指定至多 32 个输入。此时 n_总为所有输入的 n 之和。

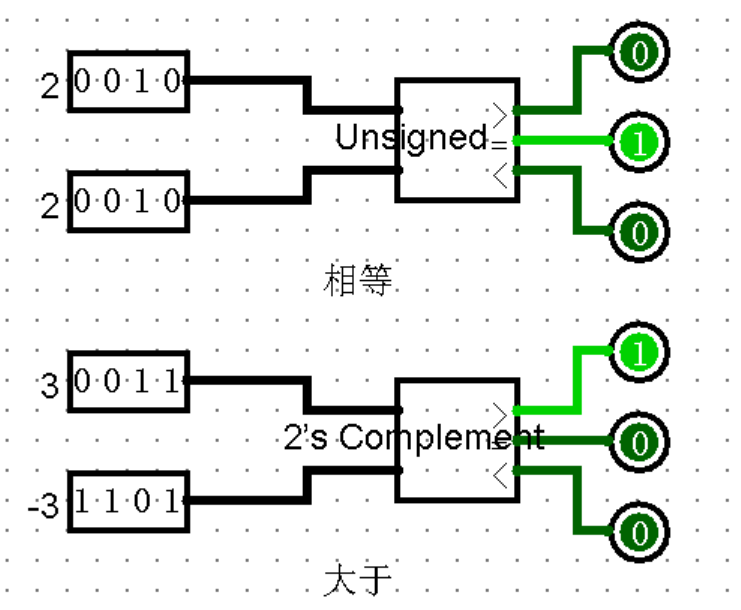
Comparator（比较）

Comparator 比较两个值（无符号值或两个补码值，可选）的大小。Comparator 有 3 个输出，通常，其中一个输出为1，另外两个输出为0。

Memory（存储）

Register（寄存器）

Register 存储单个多位值，该值以十六进制形式显示在其矩形内，并在其输出端输出。当时钟信号输入满足 Register 触发条件时，存储在 Register 中的值就会在该时刻改变为 D 输入的值。时钟信号指示 Register 储存值发生改变的确切条件是通过触发属性配置的，Logisim 中一般有时钟上升沿和下降沿，高电平和低电平这四种触发方式。

使能信号：使能信号输入为 1 时，Register 开始工作，输入信号 D 有效。使能信号输入为 0 时，Register 停止工作，输入信号 D 无效。

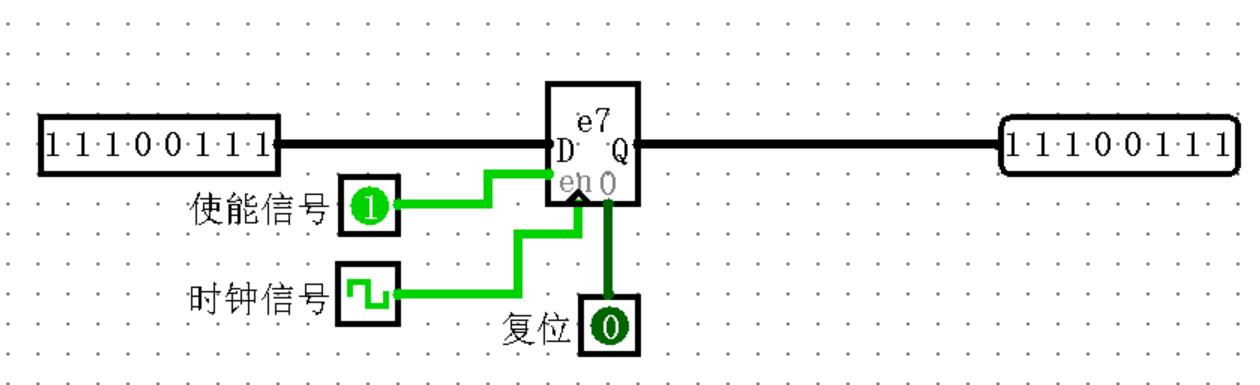
Reset（复位）输入异步地将 Register 的值重置为0（全部为0），也就是说，只要 Reset 为 1，Register 的值就固定为 0，不管时钟和输入是什么。

关于四种触发方式在周期的位置，请看此处

RAM（随机存取存储器）

在我们的实验中，我们采用的是读与写相互分离的类型，所以在选择 RAM 时，请将数据接口选择为 Separate load and store ports。

RAM 组件是 Logisim 内置库中最复杂的组件，最多可存储 16,777,216 个值（在地址位宽度/Address Bit Width 属性中指定），每个值最多可包含 32 位（在数据位宽度/Data Bit Width 属性中指定）。RAM 可加载和存储数据。此外，用户可以通过 Poke 工具 (Poke Tool) 交互修改单个值，或者可以通过菜单工具 (Menu Tool) 修改整个内容。
储存的数据值在组件中显示。地址以灰色字体形式陈列在显示区域的左边。在内部，每个值都使用十六进制格式列出。当前选定地址的值将以反色（白字黑底）显示。

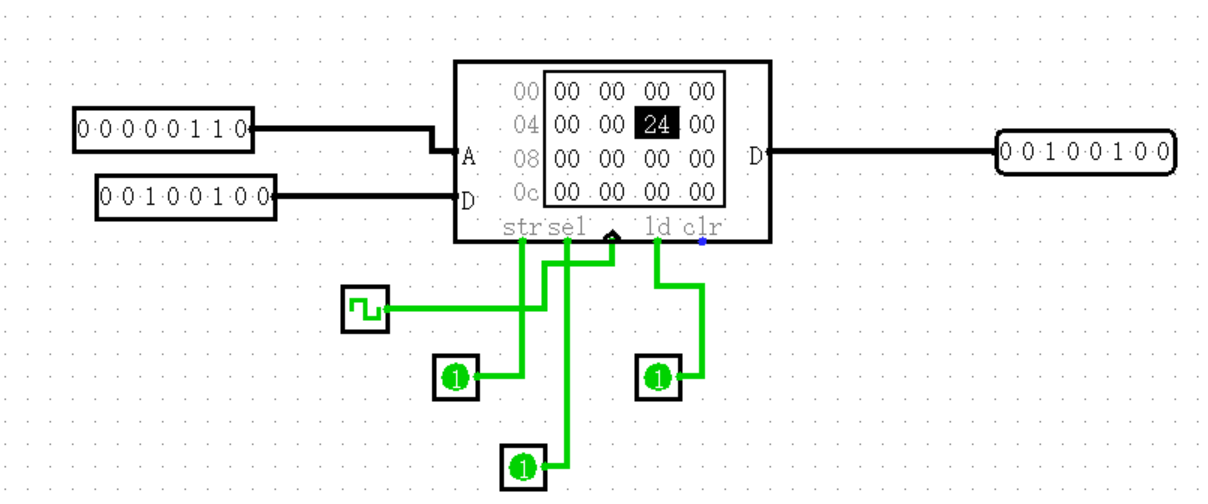
除了 clr(Clear, 为 1 时复位整个 RAM) 信号和时钟信号，sel(Chip Select, 选择生效的 RAM，即电路中同时刻只有一个 RAM 可用), str(Store, 为 1 时允许在时钟信号为高电平时将 D 输入信号写入 RAM), ld(Load, 为 1 时允许在时钟信号为高电平时从 RAM 中读取数据) 在没有输入的情况下均默认为 1。

ROM（只读存储器）

ROM 组件最多可以存储 16,777,216 个值(在地址位宽度属性中指定)，每个值最多可以包含32 位(在数据位宽度/Address Bit Width 属性中指定)。电路可以访问 ROM 中的储存值，但不能改变它们。用户可以通过 Poke 工具交互修改单个值，或者用户可以通过菜单工具修改整个内容。
与 RAM 组件不同，ROM 组件的当前内容是作为组件的属性存储的。因此，如果一个包含ROM 组件的电路被使用了两次，这两个 ROM 组件都持有相同的值。也因为这种行为，ROM 的数据存储在 Logisim 创建的文件中。
当前值显示在组件中。显示的地址以灰色显示在显示区域的左边。在内部，每个值都使用十六进制列出。当前选定地址的值将以相反的文本(白底黑)显示。

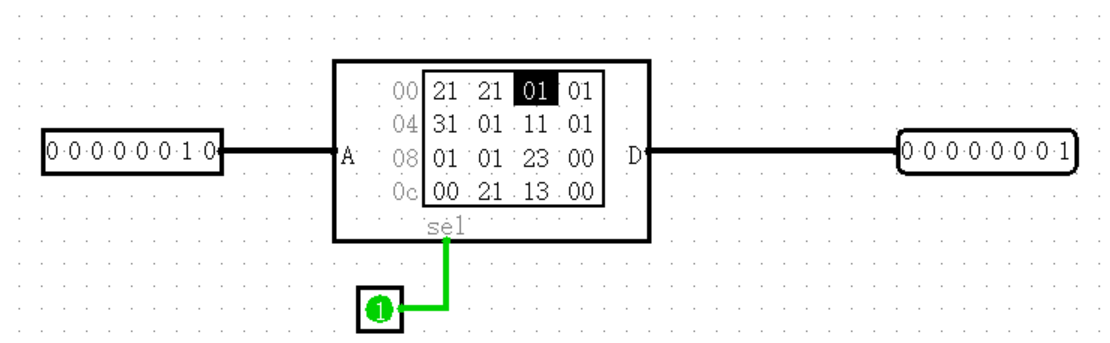
ROM 的数据是存储在本地的，以一个 .txt 形式。内含非零地址及其值，第一行固定为 v2.0 raw。

I/O（输入输出）

Base（基本组件）

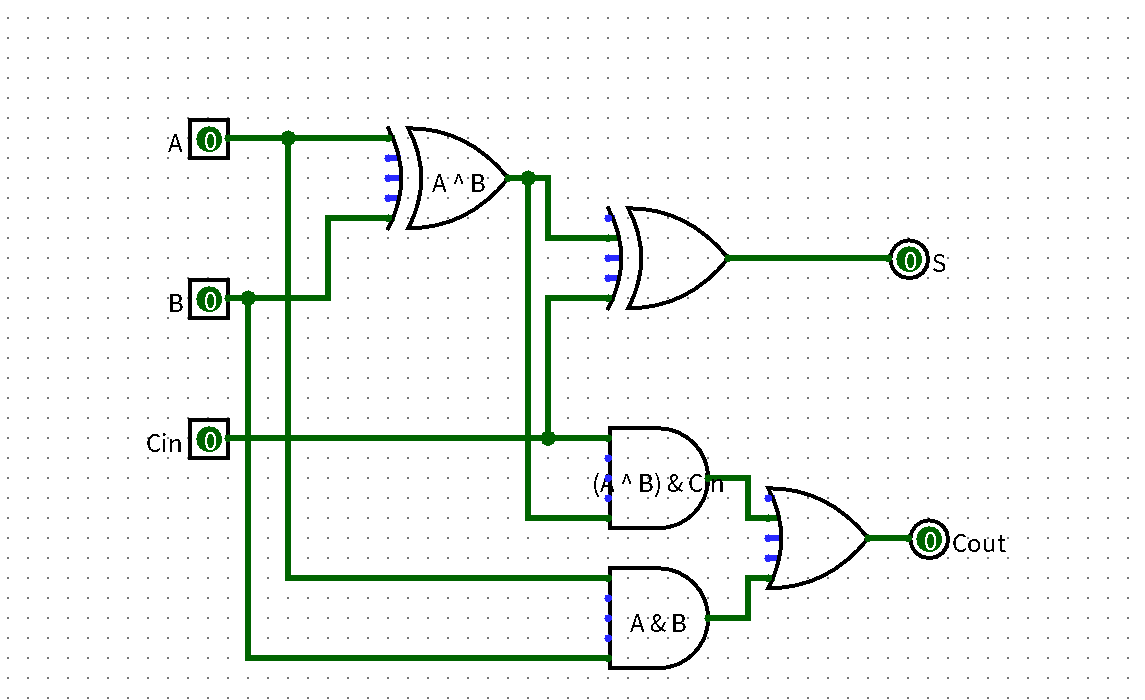
一位全加器

一位全加器由两个输入 A 和 B，一个进位输入 Cin，一个输出 S，一个进位输出 Cout 组成。全加器的表达式为：
S = A ^ B ^ Cin; Cout = A & B | Cin & (A ^ B);^[3]
对于 S 的运算，我们可以作出：^[4]
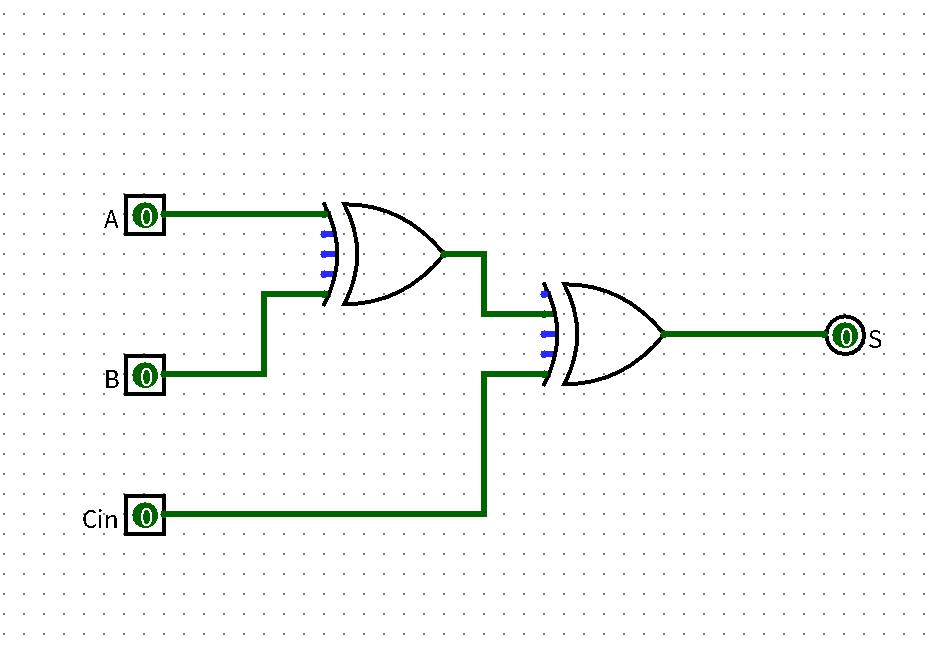利用已有的运算结果，进一步搭建整个电路：

Swap 电路

现在需要你使用基础的门电路搭建这样一个电路，当输入 S 为 0（低电平）时，输出 O1 等于输入 I1，输出 O2 等于输入 I2。当输入 S 为 1（高电平）时，则交换两输出，即输出 O2 等于输入 I1，输出 O1 等于输入 I2。我们给它取名叫做 swap 电路。

提交要求

用 Logisim 完成 swap 电路

文件内模块名：swap
输入：I1(1 bit), I2(1 bit), S(1 bit)
输出：O1(1 bit), O2(1 bit)
注意：请从门级电路开始搭建，切勿使用 Plexers 类元件。
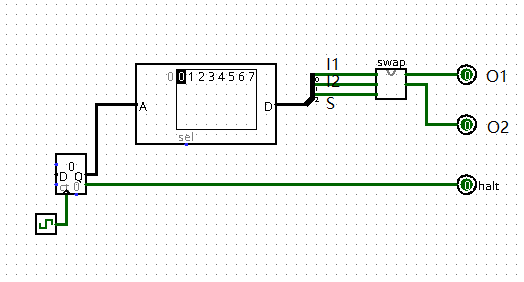
测试电路图（我们将使用下方的电路对你搭建的电路进行测试，测试的原理是将下图的 swap 模块替换为你提交文件中的 swap 模块，随后测试机会仿真运行下图中的电路图，记录其输出并与正确的输出进行对比）

模块样式：

解

答案

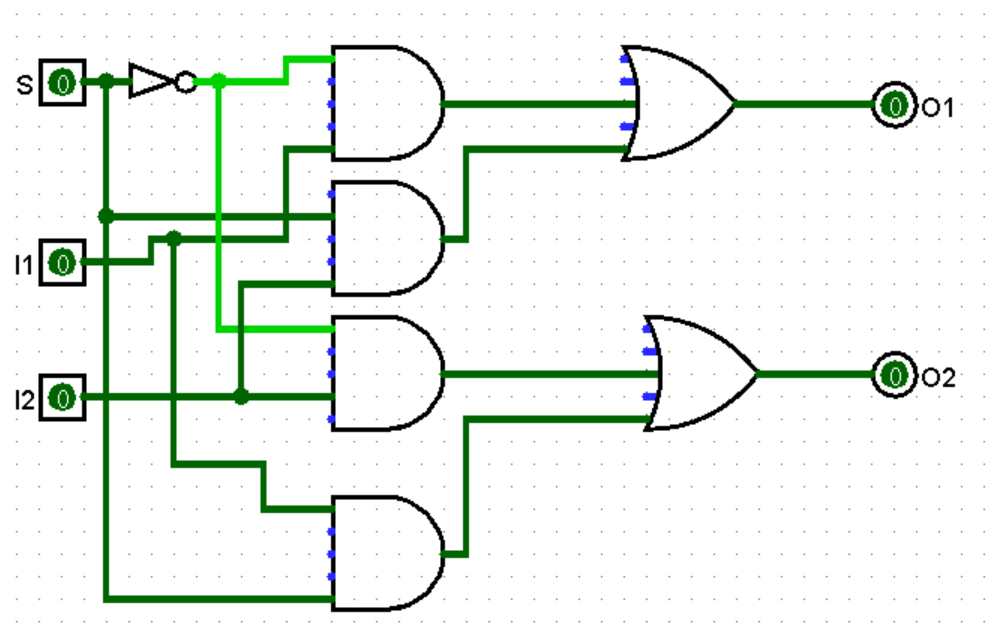
分析
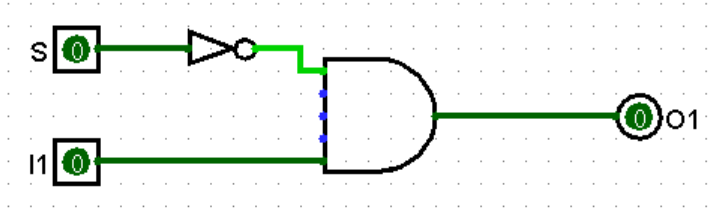
如果 S 为 0 且 I1 为 1，则 O1 为 1，若 I1 为 0，则 O1 为 0。显然，这需要一个与门来实现。

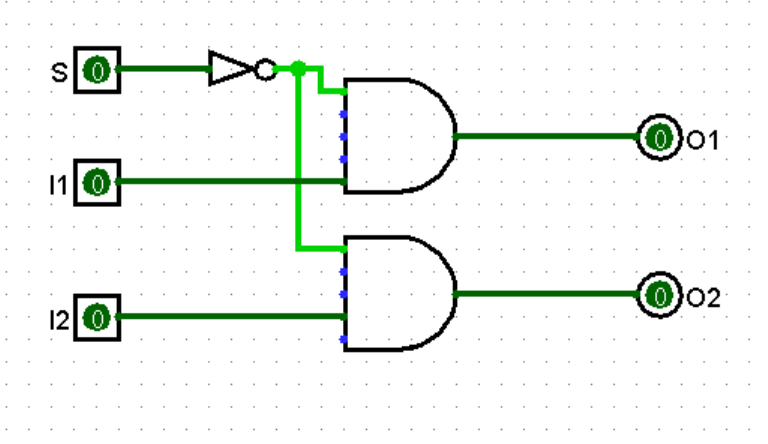
对于 I2 与 O2，是与前者一样的逻辑

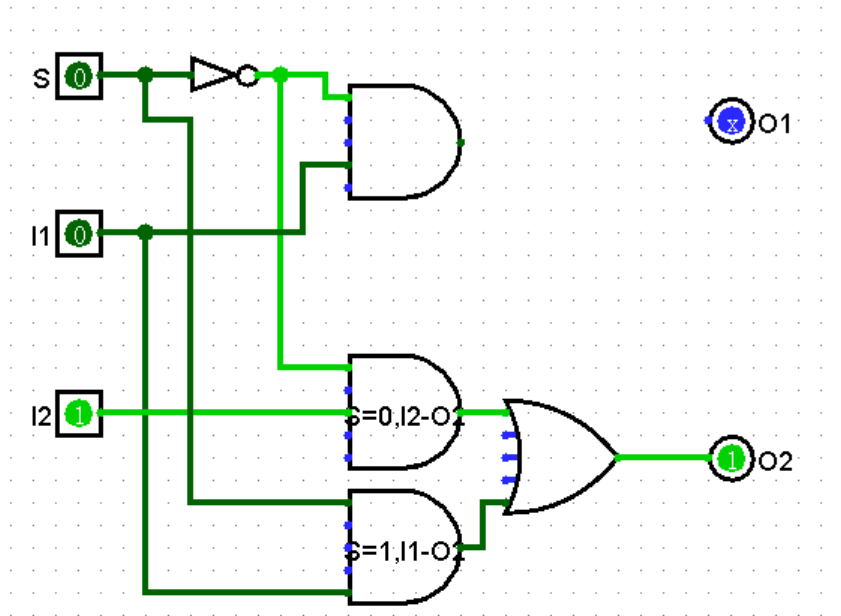
如果 S 为 1，则 I1 与 I2 的值交换再赋给 O1 与 O2。对于 I1 而言，首先必须获取其值，然后传递给 O2。由于 S 是 1，则让 S 和 I1 通过与门。考虑到 I2 到 O2 和 I1 到 O2 不会同时为 1，则将两个与门的输出用一个或门连接，再输出到 O2 即可。

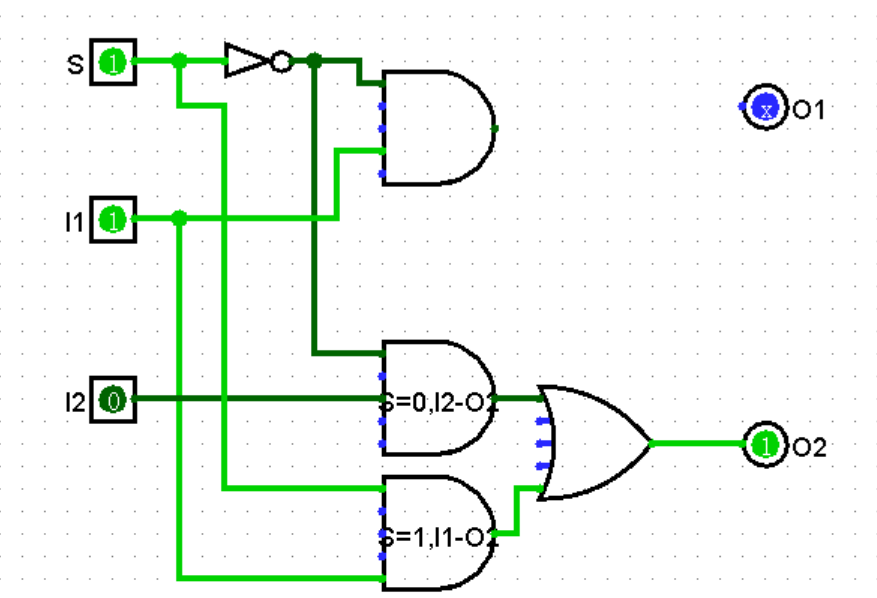
到 O1 的线路如法炮制即可。

在打包成模块时，注意按要求调整 S, I1, I2, O1, O2 的位置。
注意按要求命名。

Logisim 组合电路

子电路

子电路使用流程

创建子电路：通过 Project 栏下的 Add Circuit；
添加子电路内容；
设置外观；
引用。

譬如 Swap 电路，若将其封装成子电路，则可以设计出双重交换电路 2Swap。

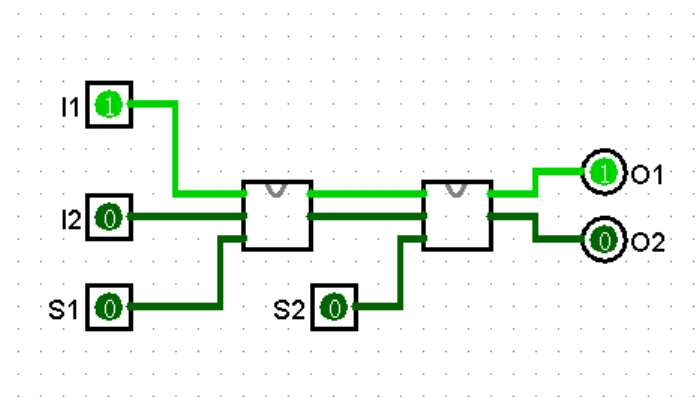
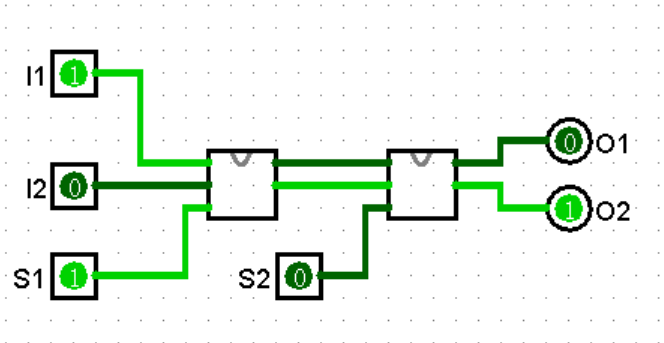
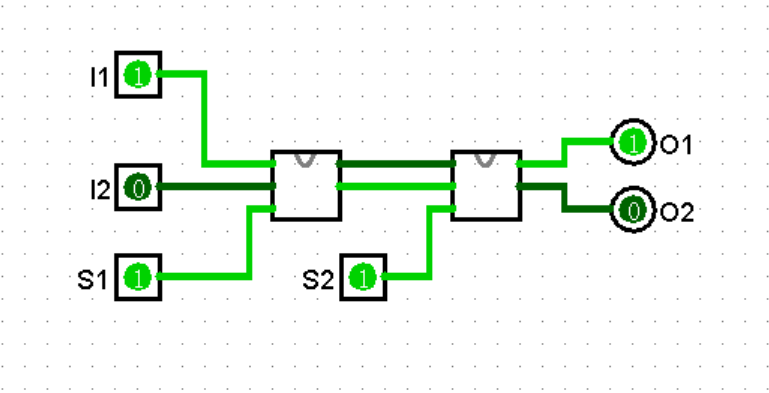
Wire Bundle（线束）

对于一个完整且正确的电路，是以深绿色，浅绿色，黑色接线构成，绿色接线可以通过深浅直接判断出取值，而黑色接线，并不能直接反映出取值，这里建议大家使用 Wiring 库中的 Probe 元器件，可以对多位数据实时显示监控。

利用 Logisim 进行组合逻辑分析

Logisim 中具有逻辑分析的功能，可以实现组合电路，真值表，布尔表达式三者间的两两转换。
打开组合逻辑分析模块的方式：

Window 栏目下的 Combinational Analysis;
Project 栏目下的 Analyze Circuit;

组合逻辑分析模块，可根据逻辑表达式得到相应的真值表。我们也可以通过输入真值表，再产生相应的表达式，或者产生相应的电路。其中真值表的选值有：0，1，x（浮动）。

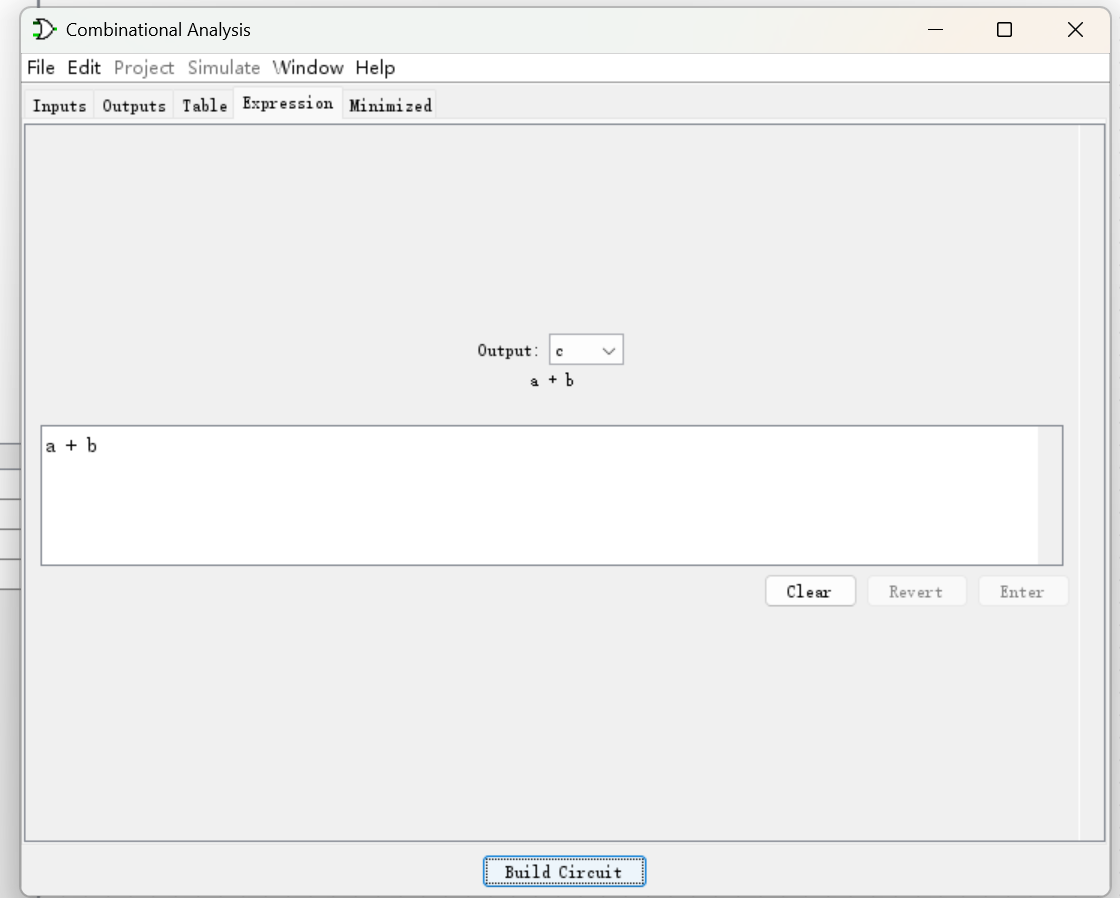
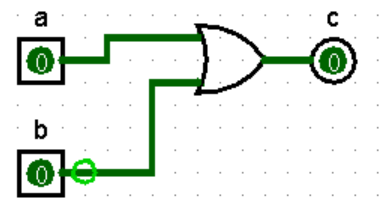
并且在生成电路时，我们也可以勾选下列生成电路的附加约束：

Use Two-Input Gates Only 只使用二输入门电路；
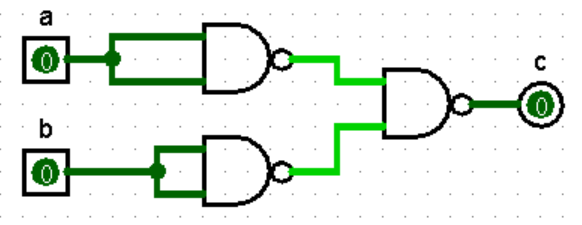
Use NAND Gates Only 只使用与非门；

排序电路（4bit_sort）

在前面的学习过程中，我们搭建了一个 1 位的 swap 电路。现在需要我们使用之前的 1 位 swap 电路来搭建一个 4 位 4 输入的排序电路。

要求

先使用 1 位的 swap 搭建 4 位的 swap，再使用 4 位的 swap 模块和 Logisim 内置的 comparator 元件搭建排序电路（请不要使用 Plexers 类元件）。

功能描述: 该电路具有 4 个 4 位的二进制数字作为输入和 4 个 4 位的二进制数字作为输出。它的功能是，将 4 个输入的二进制数字进行排序，从上往下数第一个输出端口输出的是 4 个数字中最小的，第二个输出端口输出的是第二小的，以此类推。
输入： A, B, C, D (4 bit)
输出： #1, #2, #3, #4 (4 bit)（#1 对应第一个输出端口，以此类推）
文件内 1 位 swap 模块名：1bit_swap
文件内 4 位 swap 模块名：4bit_swap
文件内排序电路模块名：4bit_sort
Hint: 所有的二进制数字均看做是无符号的。

解

1 位 swap 电路可以参考这里。
要构建 4 位 swap 电路，其实就是把 4 bit 输入拆分成四个 1 bit 输入，然后分别交给 1 位 swap 电路，再将四个 1 bit 输出连接起来即可。拆分，也就是使用 Splitter 元件，交换后再用 Splitter 连接起来。有关 Splitter 您可参考这里。

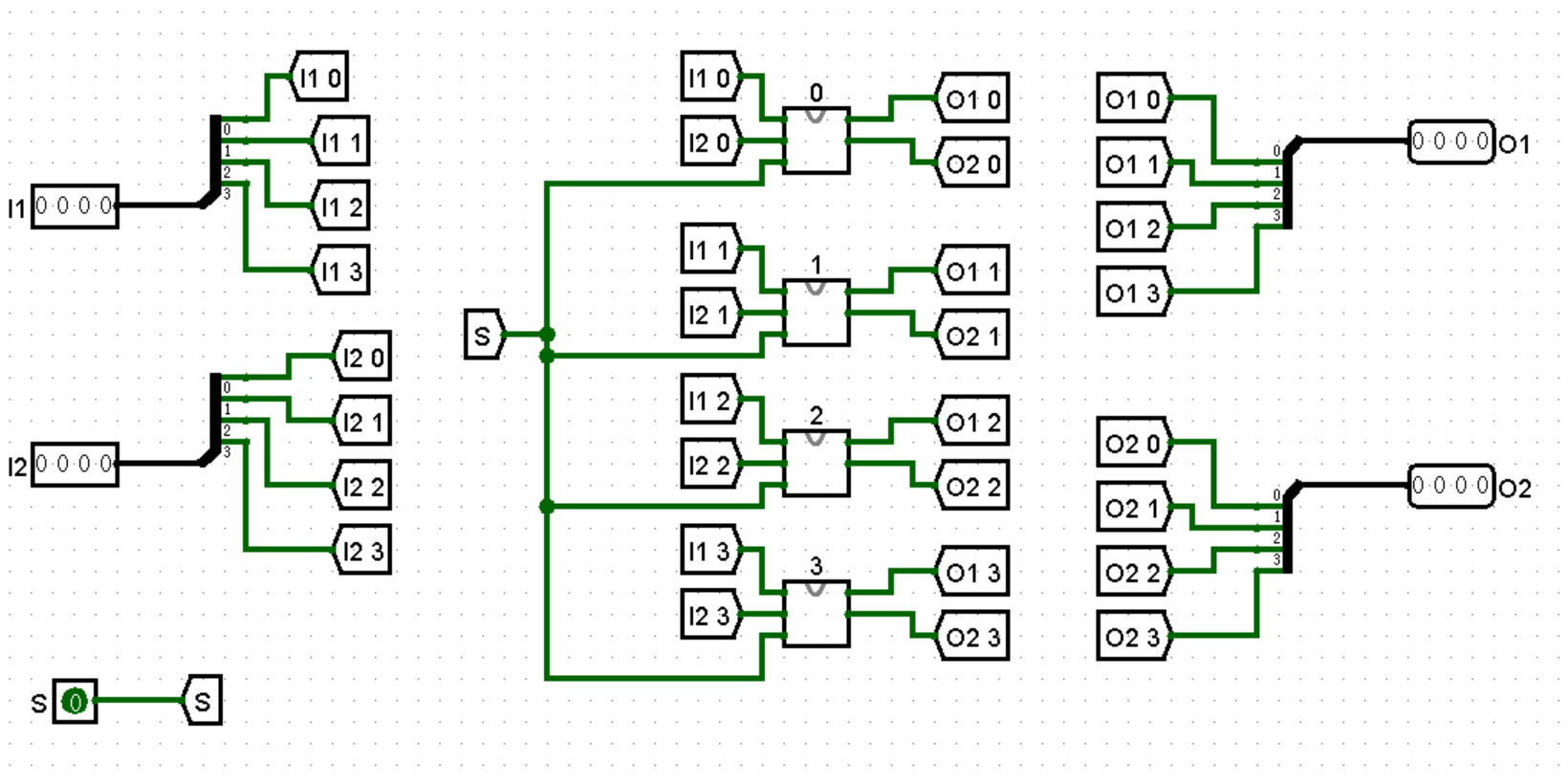
注意
图中已封装好的模块是 1 位 swap 模块 1bit_swap。

您可使用 Tunnel 元件简化电路。关于 Tunnel 元件您可参考这里。

如何实现排序呢？我们可以使用冒泡排序（Bubble Sort）来完成。对于 A, B, C, D 四个输入，我们可以先比较 A 和 B 的大小，由于要求从小到大输出，那么如果 A > B，则交换 A 和 B，然后比较 A 和 C，如果 A > C，则交换 A 和 C，以此类推，直到比较完所有四个输入。每个输入都会与另三各完成一次比较，从而得到四者的顺序。此处我们可以充分利用 Tunnel 元件，将一次比较的结果传递给下次比较的输入。

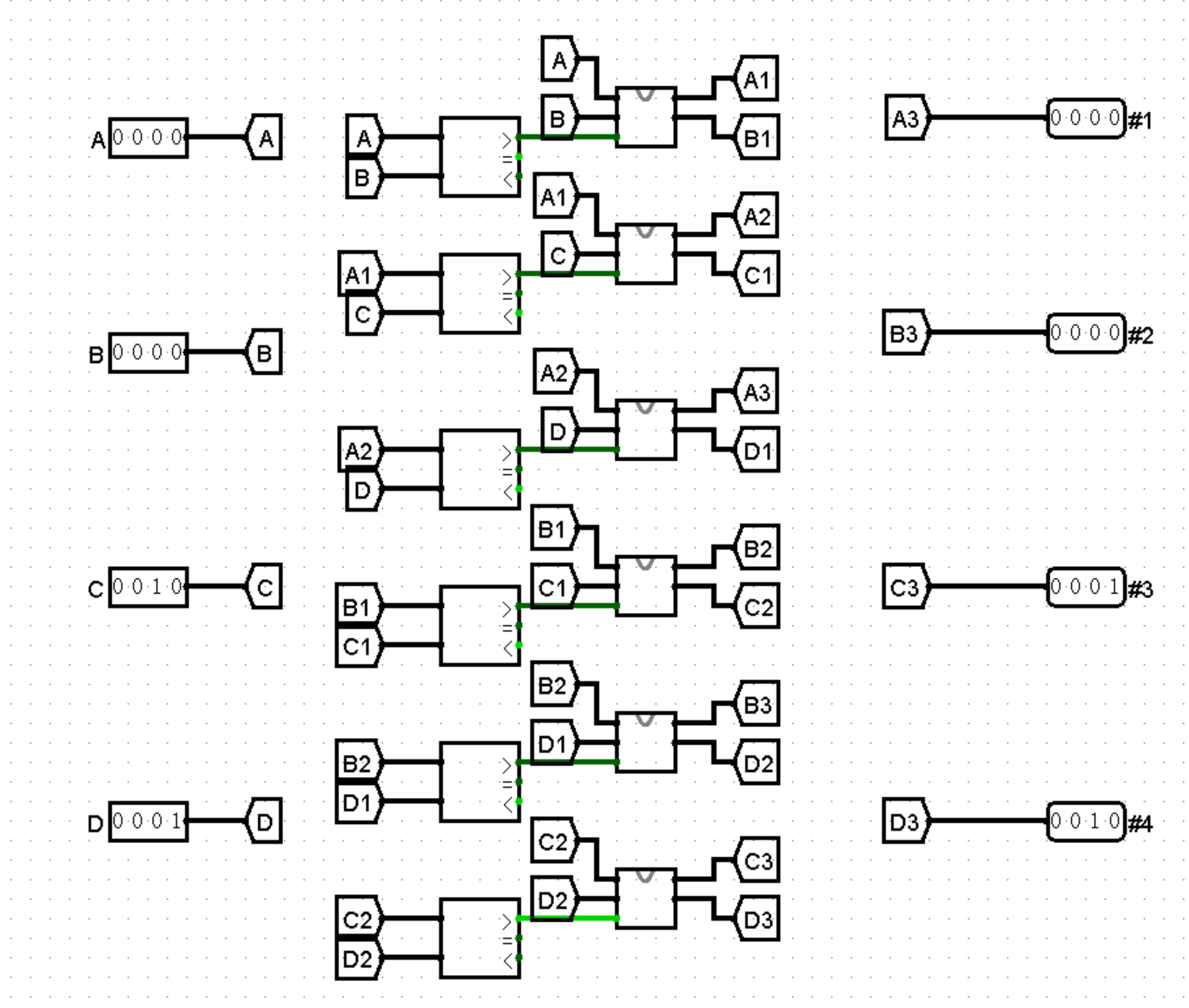
注意
图中已封装好的模块是 4 位 swap 模块 4bit_swap。

每轮比较，若结果为大于，则 Comparator 输出 1，该信号作为使能信号激活 4bit_swap 模块，将输入的二者交换。完成后，其结果用新的 Tunnel 传递给之后的比较轮次。

Logisim 时序电路

SR 锁存器（SR Latch）

部分内容选自知乎。

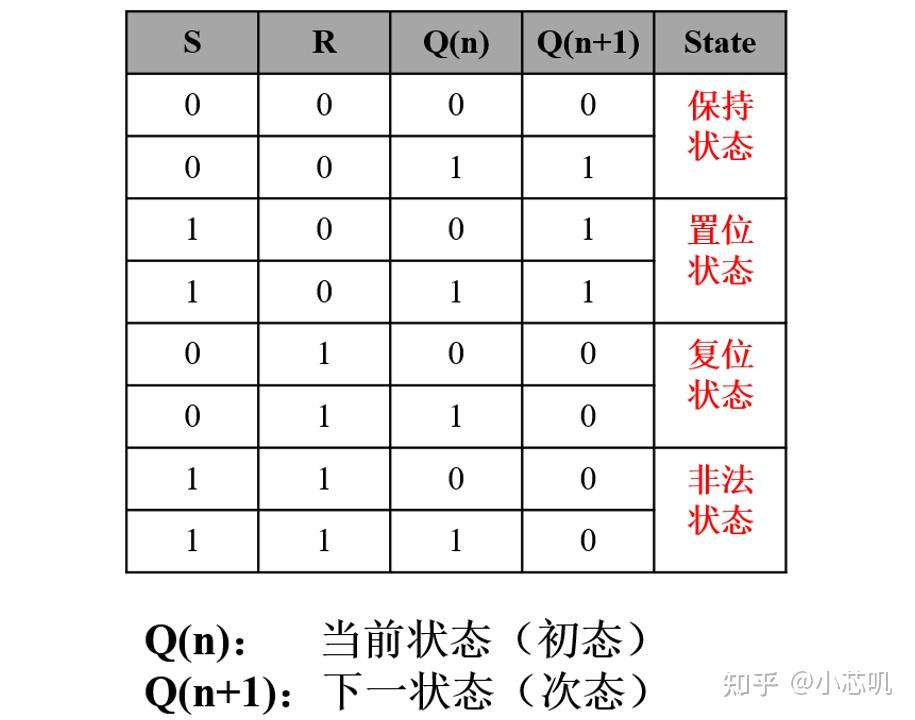
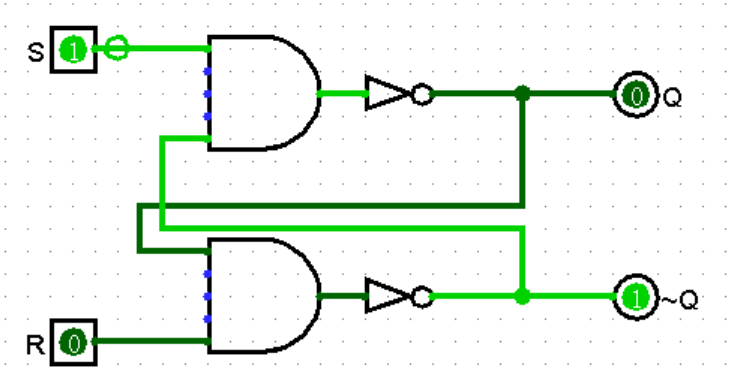
我们先来讲解一种简单的电路——SR 锁存器（SR latch），它由两个交叉耦合的或非门（或者，等价地，两个反置输入的与非门）组成，整个电路的状态可以由 S（Set）和 R（Reset）输入来决定，对应得到两个相反的输出 Q 和 ~Q，它的真值表如下：

一种电路如下：

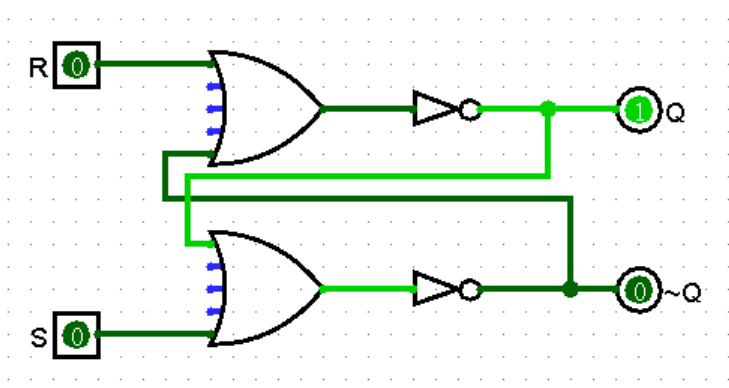
Q 为 1 而 ~Q 为 0 时被称为锁存器的 1 状态，Q 为 0 而 ~Q 为 1 时被称为锁存器的 0 状态。

其中 S_D 和 R_D 为是电路输入的两个端口，Qⁿ 表示电路当前的输出，Qⁿ⁺¹ 表示电路下一个状态的输出。由真值表可以看出，这个电路的输出不仅和当前输入有关，也和上一次的输出有关。
观察它的功能一栏，可以看到，通过改变 S_D 和 R_D 为合适的值，我们可以改变电路的输出，而当 S_D 和 R_D 为均为 0 时，电路会一直保持原来的输出不变，这看上去很像 U 盘之类的设备（通电时能够修改存储的内容，断电时保持内容不变）。事实上，通过配合合适的外部电路，我们就可以使用这个电路来存储整个电路的状态，从而搭建起更复杂的时序电路。

简单来说，初始情况下 S 和 R 均为 0，按下 S 键，锁存器将进入 1 状态(Set)。此时，无论 S 如何变化，锁存器的输出都将不变。因为锁存器已经被设置成 1 了。再按下 R 键，锁存器重置（Reset），输出变为 0。无论 R 如何变化，锁存器的输出都将不变。因为锁存器已经被重置了。0 重置仍然是 0。

由于复位和置位都是输入端为 1 才发生，故这种 SR 锁存器叫做高电平有效的SR锁存器。

还有一种低电平有效的SR锁存器，它的输入端 S 和 R 均为低电平有效。真值表如下：

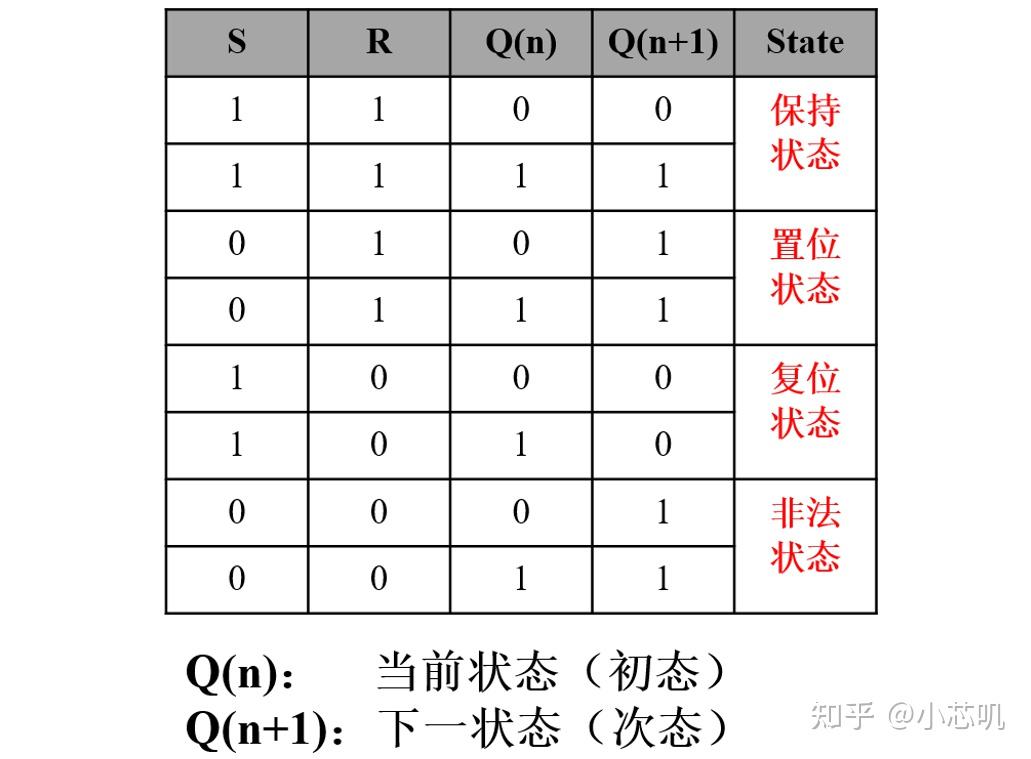
它的电路如下：

D 锁存器（D Latch）

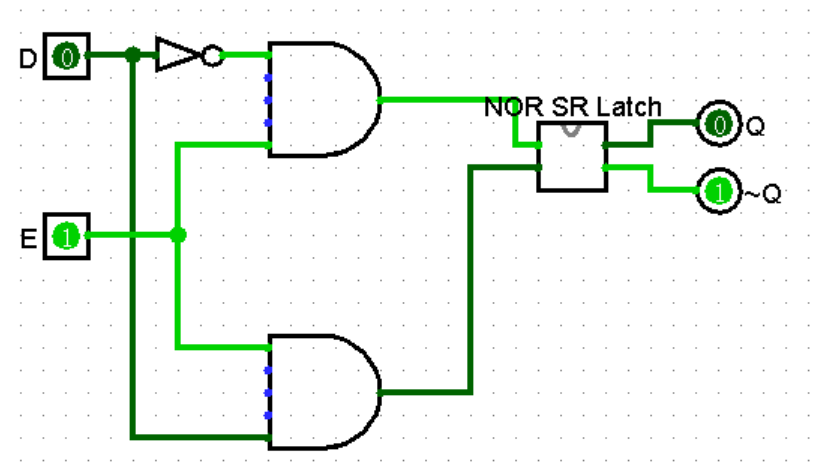
D 锁存器是最常用于在数字系统中存储数据的逻辑电路。它基于 SR 锁存器，但没有“未定义”或“无效”状态问题。

注意
图中封装的电路是高电平有效的SR锁存器。

D 锁存器有两个输入 D 和 E，其中 E 是使能信号。当 E 为 1 时，D 锁存器将 D 输入的值存储在 Q 中，随着 D 变化而变化。当 E 为 0 时，D 锁存器保持当前的 Q 值不变。即锁存 D 输入的值。

E 也可以看作是 CLK 时钟信号。此时 D 锁存器将时间输入和数据输入明确的分隔开，而 SR 锁存器是没有区分的。
当 CLK 为 1 时，D 锁存器是透明的（transparent），数据 D 通过 D 锁存器流向 Q。当 CLK 为 0 时，D 锁存器是不透明的（opaque），其阻塞新数据流向 Q，Q 保持原值不变。

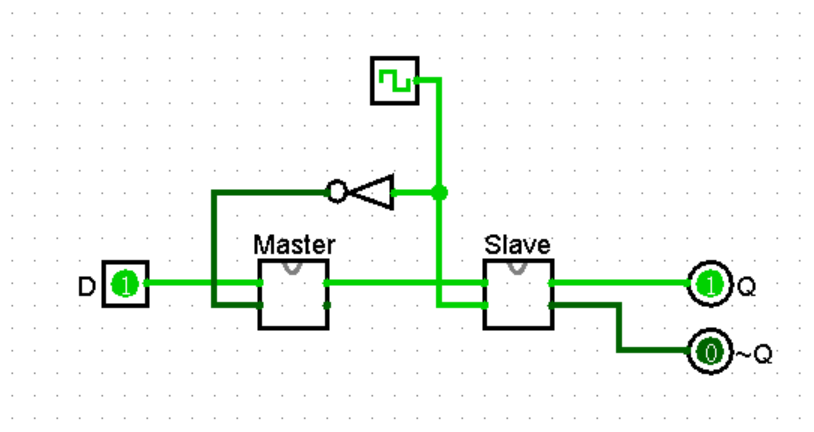
D 触发器（D Flip-Flop）

D 触发器由反相时钟控制的两个 D 锁存器组成。分别为主锁存器（Master）和从锁存器（Slave）。
CLK 为 0 时，主锁存器透明，从锁存器不透明，D 流向从锁存器但无法流入，保持在二者连线处。CLK 为 1 时，主锁存器不透明，从锁存器透明，数据流向 Q，但新的输入无法流入主锁存器。
也就是说，D 触发器只会在时钟上升沿将 D 复制到 Q，在其他时间段保持原来的状态。

有限状态机（FSM）

有限状态机的定义和行为

有限状态机的构成和基本性质

有限状态机（Finite State Machine，FSM）又称有限自动状态机，它拥有有限数量的状态，每个状态代表不同的意义，每个状态可以切换到零-多个状态。任意时刻状态机有且只能处在一个状态。

数学定义
构成一个有限状态机的六元组为：状态集合，输入集合，输出集合，状态转移函数，输出函数，初始状态。给定以上六个集合，函数或元素，就可以确定一个有限状态机。

据此，有限状态机具有以下特征：

在任何时间点，状态、输入、输出均为给定的有限种情况之一。
对于一对确定的当前状态和输入，只有一个固定且唯一的次态（下一个周期的状态）。
对于一对确定的当前状态和输入，只有一种固定且唯一的输出情况。

有限状态机的时序行为

状态转移行为可以描述成如下过程：

当第 0 周期开始，状态设定为 state₀。
第 n 周期结束的瞬间，记此时刻输入为 input_n。
每当第 n 周期结束，第 n + 1 周期开始时，状态变为状态转移函数给出的次态：state_n+1 = F_next(state_n, input_n)。

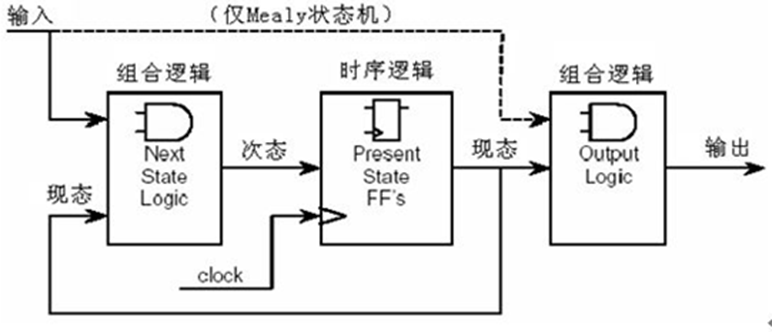
Moore 和 Mealy 状态机的区别

区分状态机类型时：当输出函数的结果会随 input 变化而改变时，该状态机为 Mealy 机，否则为 Moore 机。

2ⁿ mod 5

要求

使用 Logisim 搭建电路，该电路串行输入一个二进制无符号数 B（先从高位输入，每输入一个数字就相当于之前输入的数左移一位再加上当前输入的数字），输出 “2 的 B 次幂” 模 5 的余数的电路并提交。

输入： In（1bit 串行输入）
输出：S₀, S₁, S₂, S₃, S₄ （独热编码，S_x 为 1 时表示 2^In ≡ x (mod 5)）
文件内模块名: mod5
状态机类型: Mealy 型有限状态机
注意：切勿使用内置算术器件（如加法器、除法器等）！请搭建有限状态机！
样例：输入输出样例中每一行表示相邻上升沿之间的开区间时间内的输入和期望输出。

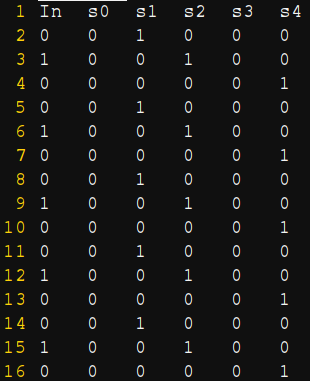
解

题目要求使用有限状态机来搭建，且由于输入和输出有关，是 Mealy 型状态机。
首先要确定状态集合。2 的幂次方模 5 所产生的余数其实只有 1 到 4，也就是说只有四种状态。我们可以用 2 位的二进制数来表示状态：

状态	余数
00	0
01	1
10	2
11	3

不难发现，1 % 5 = 1, 2 % 5 = 2, 4 % 5 = 4, 8 % 5 = 3, 16 % 5 = 1……即余数以 4 为周期进行循环。若把被除数写成二进制形式，并观察其末二位，则会发现有这样的规律：

余数	状态	末二位	被除数
1	00	00	2⁰
2	01	01	2¹
4	11	10	2²
3	10	11	2³

现在，要改变状态，我们会进行一次输入，考察这次输入引起的变化：末二位左移一次，输入值填补在低位。输入只有 1 和 0 两种情况，而现在状态有 4 种，因此我们可以枚举出共计 8 种可能的情况：

接下来，现在状态的第一位称为 ST1，第二位为 ST2；次态的第一位称为 ST1’，第二位为 ST2’；输入称为 IN；余数称为 S0 到 S4。

状态转移表如下：

ST1	ST2	IN	ST1’	ST2’	S1	S2	S3	S4
0	0	0	0	0	1	0	0	0
0	0	1	0	1	0	1	0	0
0	1	0	1	1	0	0	0	1
0	1	1	1	0	1	0	1	0
1	0	0	1	1	0	0	0	1
1	0	1	1	0	0	0	1	0
1	1	0	0	0	1	0	0	0
1	1	1	0	1	0	1	0	0

可以看出 S0 恒为 0。

根据 Mealy 型状态机的结构图，我们需要构建三个部分：状态转移逻辑、输出逻辑和寄存器。其顶层结构如下：

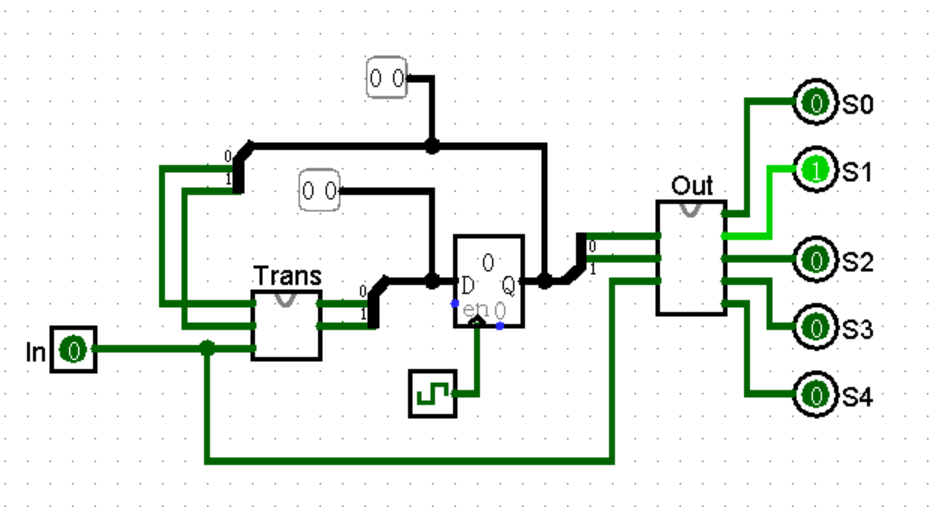
寄存器保存的是现态。在上升沿以外的时间段，可以把整个状态机的行为拆分成两步：

现态从 Q 流向状态转移逻辑 Trans，和 In 一起决定次态的值。但是由于时间在上升沿以外，次态滞留在寄存器外，无法改变其值。
现态从 Q 流向输出逻辑 Out，和 In 一起决定输出的值。

当时间来到上升沿，滞留的次态值进入寄存器，完成状态的转移。然后在下一个上升沿到来前，重复上述的 1 和 2 步。

这正好满足了样例说的“每一行表示相邻上升沿之间的开区间时间内的输入和期望输出”，因为输出这一步骤就是在两个上升沿之间完成的。

状态转移逻辑和输出逻辑的实现，最简单的步骤就是根据状态转移表，使用 Logisim 的 Analyze Circuit 功能来自动生成即可。

斐波那契数列

要求

使用 Logisim 搭建一个根据输入序号 x 计算对应序号斐波那契数 F_x 的电路并提交。

F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2 (n ≥ 2)
输入：N (3bit)
输出：Nth(4bit)
文件内模块名: main
测试要求：每次给定一个固定输入保持不变，电路在 64 个周期内计算出结果并稳定输出，在结果未计算出之前输出端口输出 0。

解

计数逻辑

要知道第 x 号斐波那契数的值，我们可以从 0 号和 1 号开始，依次计算斐波那契数，直至第 x 号时停止并输出。那么要算多少次呢？如果我们以 0 号和 1 号开始，每一个时钟周期计算一次的话，那么第一个周期算出 2 号，第二个周期算出 3 号……并且，还需要花掉一个上升沿去初始化寄存器的值，计数器达到需求时，又需等下一个上升沿才能输出结果。若要求 2 号斐波那契数，计数逻辑到第 3 个上升沿时就会发出停止运算并输出的信号。而第 1 个上升沿被用来初始化，第 2 个上升沿算出 2 号，到第 3 个上升沿算出 3 号，输出的结果就是 3 号斐波那契数了，并不符合我们的需求。因此我们可以往前推一位，以 -1 号和 0 号开始。

F_-1 = 1, F₀ = 0。

这样，第 x 号斐波那契数需要 x 个时钟周期才能算出。换言之，当第 x 个时钟周期结束时，已经算出了第 x 号斐波那契数。而下一个时钟周期的上升沿，必须停止计次，然后输出数字，否则会多算一次。
控制运算次数的逻辑可以使用一个计数器（Counter）和一个比较器（Comparator）来实现。计数器从 0 开始，每到一个上升沿加 1。也就是说 x 个时钟周期结束时，计数器的值为 x，在下一个上升沿到来时，传递一个信号（output_signal）给运算斐波那契数的逻辑，令其做完运算后立刻输出结果，并且将结果锁定在寄存器中。每个上升沿，用比较器比较计数器的值和 N 的值，若计数器的值小于等于 N，则 output_signal 为 0，否则为 1。

由于输入格式是 3bit，若计数器的位宽也设置成 3bit，则会在边界情况下失效。比如输入为 111，第七个周期时，计数器的值为 111。在下一个上升沿到来时，计数器的值要么回到 000，要么保持 111，始终无法让其大于输入值，output_signal 始终为 0。因此，需要设置计数器的位宽比输入值多 1 位。然后使用 Bit Extender 把输入扩展到 4bit。

比较器的 Numeric Type 参数必须设定为 Unsigned 即无符号数比较。若为 2's Complement 即补码比较，则 output_signal 会逆转。

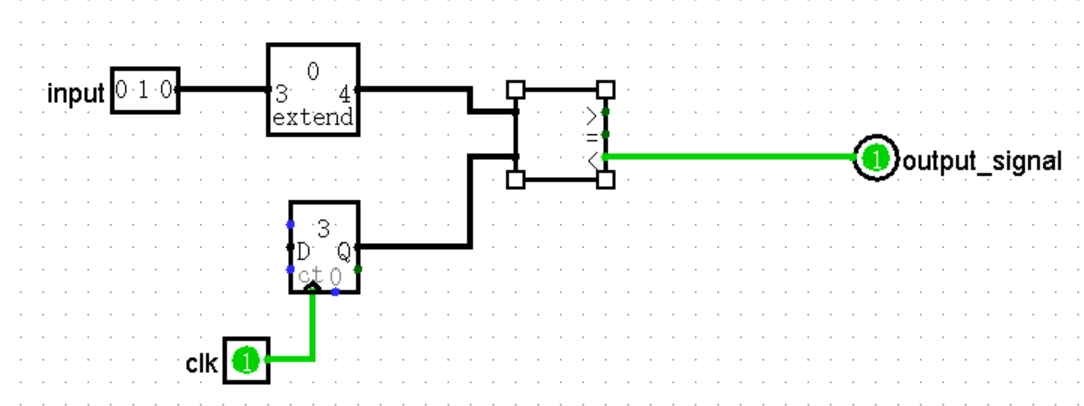
运算逻辑

回到运算斐波那契数的逻辑。由于每个斐波那契数的值只与其前两个值（prev, cur）有关，每次算出新值 = prev + cur，可以用 cur 覆盖 prev，然后用新值覆盖 cur，以此类推就可以持续计算下去。这些步骤在上升沿完成。核心逻辑如下：

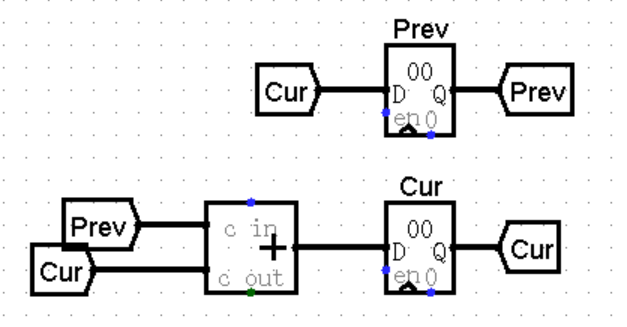
在上升沿以外的时刻，Cur 值流向 Prev 寄存器，但无法进入，滞留在线路中。同时 Prev 和 Cur 值在 Adder 中相加，得出下一个斐波那契数，流向 Cur 寄存器，也无法进入，滞留在线路中。
在上升沿，Cur 值进入 Prev 寄存器，并覆盖原有值，同时新的斐波那契数进入 Cur 寄存器，覆盖掉原有值。也就是说，最新的斐波那契数保存在 Cur 寄存器中，并且是每个上升沿到来时更新一次。

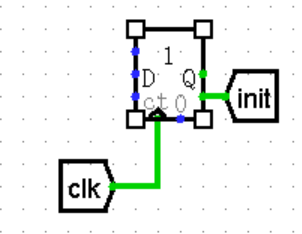
如何初始化两个寄存器呢？由于 F_-1 = 1, F₀ = 0，因此我们要把 Prev 寄存器的值设为 1，而 Cur 寄存器默认为零。我们用一个 Maximum Value 为 1 的计数器来实现。利用到计数器有一个 Carry 输出，当计数器达到最大值时，Carry 输出为 1，否则为 0。再搭配一个二选一 MUX，0 号输入为想要的初始值，1 号输入则是 Cur 隧道。这样就实现了如下效果：

第一个上升沿到来前，MUX 选择初始值，但无法进入 Prev 寄存器，滞留在线路中。
第一个上升沿到来时，初始值进入 Prev 寄存器，实现初始化。MUX 选择 Cur 隧道值。

锁定斐波那契数

很简单，传入 output_signal，当其为 1 时表示已经算出了所求的，让其通过非门，然后传给两个寄存器的使能信号端口即可。

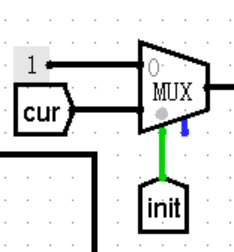
稳定输出

在找到要求的斐波那契数前，输出 Nth 要求保持为 0。可以用一个二选一 MUX，0 号输入为 0，1 号输入为 Cur 隧道值。传入 output_signal，当其为 1 时自然就输出了 Cur 寄存器中保存的值。

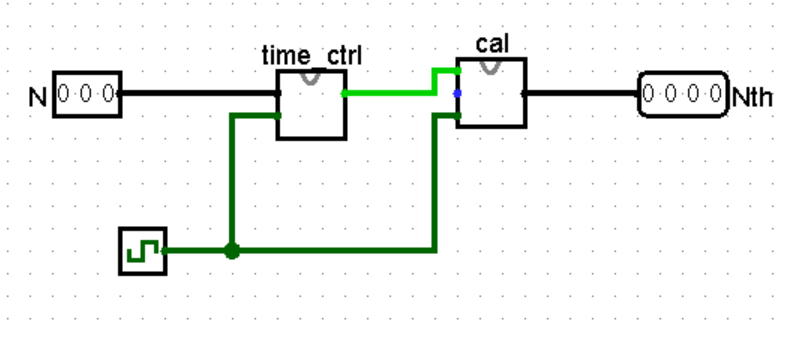
整个运算逻辑如下：

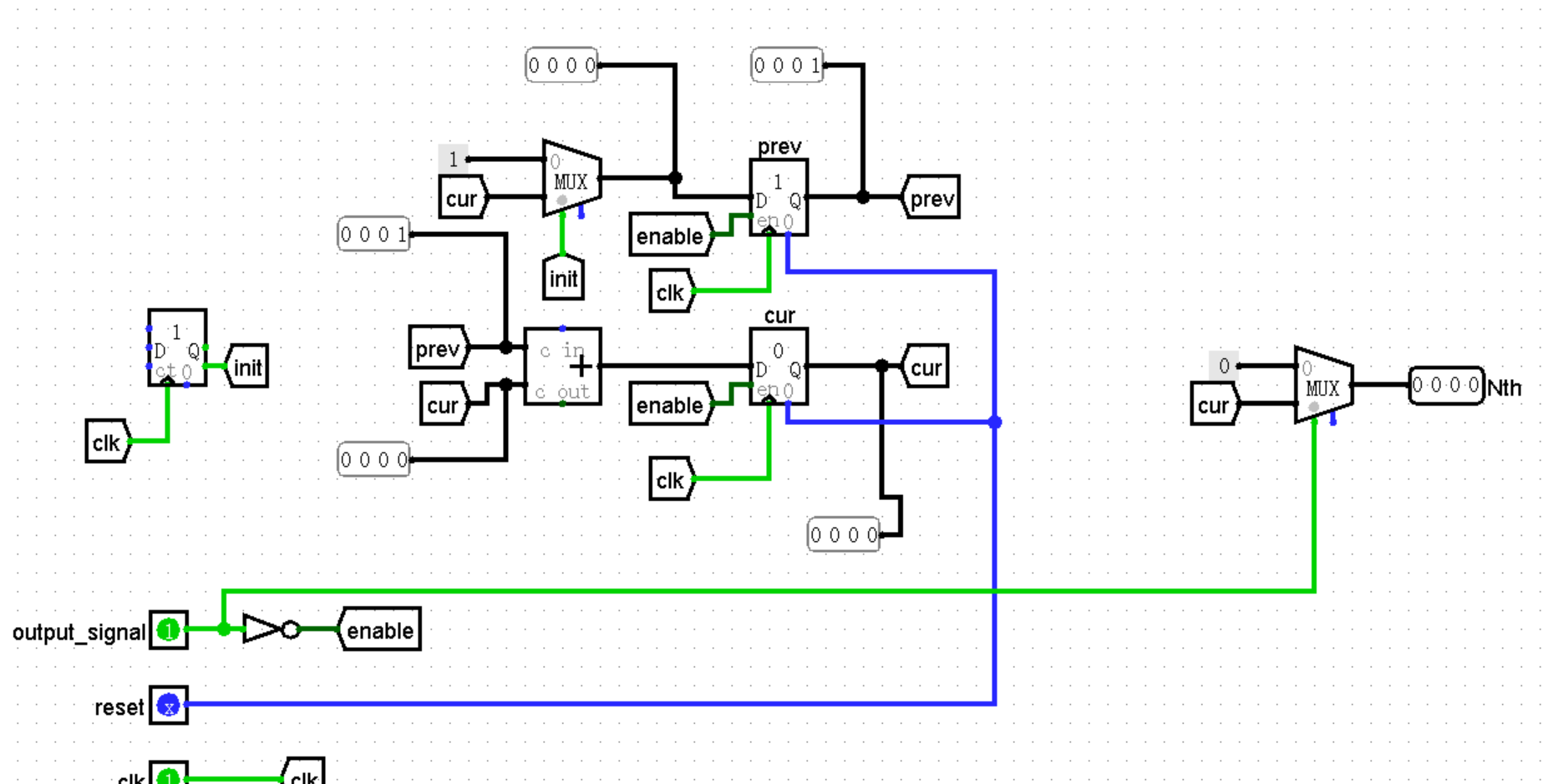
顶层电路如下：

Tunnel 需要增加标签以区分不同的数据。并且每个标签只允许有一个输入，输出的数量不做限制。但是在有较多 Tunnel 部件的时候，要特别留意标签的名字，防止出现混乱。 ↩︎
将输入数据的最高位视为符号位，扩展的数值全为符号位的值。 ↩︎
优先级：& > ^ > | ↩︎
Logisim 画布上，高亮代表此线路的真值为 1，不高亮代表此线路的真值为 0。 ↩︎

ST1	ST2	IN	ST1’	ST2’	S1	S2	S3	S4
0	0	0	0	0	1	0	0	0
0	0	1	0	1	0	1	0	0
0	1	0	1	1	0	0	0	1
0	1	1	1	0	1	0	1	0
1	0	0	1	1	0	0	0	1
1	0	1	1	0	0	0	1	0
1	1	0	0	0	1	0	0	0
1	1	1	0	1	0	1	0	0

ST1	ST2	IN	ST1’	ST2’	S1	S2	S3	S4
0	0	0	0	0	1	0	0	0
0	0	1	0	1	0	1	0	0
0	1	0	1	1	0	0	0	1
0	1	1	1	0	1	0	1	0
1	0	0	1	1	0	0	0	1
1	0	1	1	0	0	0	1	0
1	1	0	0	0	1	0	0	0
1	1	1	0	1	0	1	0	0

序